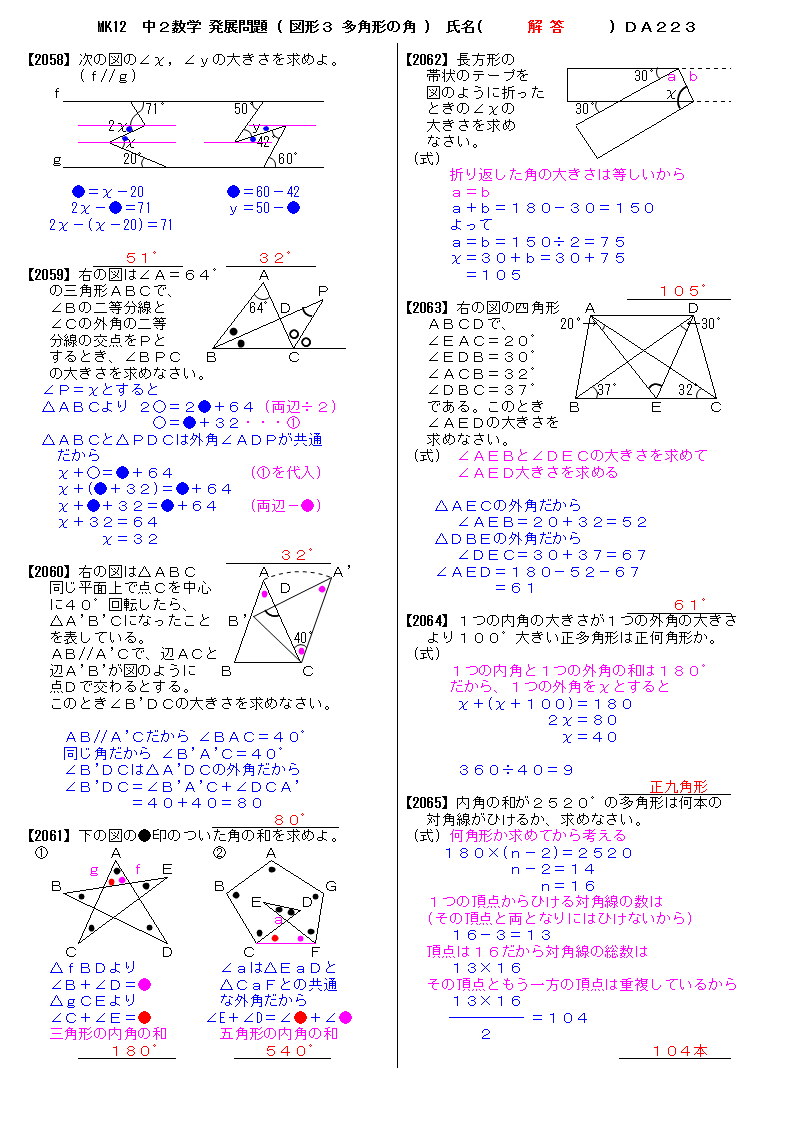
星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e) 赤 の内角の和: 180° 緑 赤 の内角の和: 360° ( 180° 180° ) 緑赤の内角の和は360°だよね?これって、結局、四角形の内角の和のことを言っているわけ! ほんじゃ次! 五角形の内角の和 答えは、540°なんだ。 同じように五角形の内角の和を考えてみる!多角形の内角の和は? 多角形の内角の和は、下記の公式で算定します。 多角形の内角の和=180×( n-2) nは多角形の辺の数です。多角形のnの値を下記に示します。 三角形 ⇒ n=3 四角形 ⇒ n=4 五角形 ⇒ n=5 六角形 ⇒ n=6
N 边形内角和 西瓜视频搜索
多角形内角和
多角形内角和-三角形の内角の和は何度か。 x角形の内角の和は何度か。 十角形の内角の和は何度か。 正八角形の一つの内角は何度か。 次の問いに答えよ。 二十角形の内角の和は何度か。 十八角形の内角の和は何度か。 内角の和が 7°になるのは何角形か。 多边形的内角和与外角和ppt,例1求八边形的内角和的度数. 解 (n-2)×180° =(8-2)×180° =1 080° 例2已知多边形的内角和的度数为900°,则这个多边形的边数为_____ 解 (n-2)×180° = 900° (n-2)= 900° /180° (n-2) = 5 n= 5 2 n=7 例3 已知在一个十边形中,九个内角的和的度数是1290°,求这个十边



如果一个多边形的内角和与外角和相等则此多边形是 X题卡
内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い 多边形的内角和计算方法: 设多边形的边数为n。 则其外角和=360°。 因为n个顶点的n个外角和n个内角的和=n*180°(每个顶点的一个外角和相邻的内角互补)。 所以n边形的内角和; =n*180°-360°; =n*180°-2*180°; =(n-2)*180°;・内角の和=180×(n-2)=180×(5-2)=540度 どうですか?五角形の内角の和は540度で間違いないですよね? したがって、 n角形の内角の和=180×(n-2) となるのです。これが 公式 です
以上のことから、多角形の内角の和は下の 公式 で求められます。 多角形の内角の和 = 線を引いて現れた三角形の数 × 180 これをもっと簡単な公式にします。1つの内角の大きさ : 3240°÷=162° 1つの外角の大きさ : 180°-162°=18° もしくは 360°÷=18° ≪答≫ 内角の和:3240°, 1つの内角の大きさ:162°, 1つの外角の大きさ:18° 練習問題4 内角の和が以下のようになる多角形を答えなさい。 1 360 Python turtle 画正多边形和多角形作正多边形作正多角形计算内角画图代码作棱角分明的多角形观察棱角分明的多角形简洁的结论代码高斯与正十七边形作出正十七角形思考原创文章,转载请申明出处作正多边形正n边形的内角和:x = (n 2) * 180° / nimport turtle# 正n边形参数n = 7x = (n 2) * 180 / n# 调整画笔
正多角形の1つの内角の大きさを出したいときは、 内角の和を頂点の数でわればいいんだ。 内角の和「180°×(n2)」を、 頂点の数「n」でわると正多角形の1つの内角の大きさになるよ。 180× (n2)/n どの内角も同じ大きさだからね! 予習シリーズ小5上第1回と対応します。必修レベル内角の和・外角の和 五角形の内角の和は、何度か。 正五角形の1つの内角の大きさは、何度か。 内角で求めるか、外角で求めるかの2パターンある。内角で求める解き方1つの角度を聞い手机看 三角形内角和转笔法 当前播放至 0000 扫一扫 手机继续看 iPhone客户端 iPad客户端 Android客户端 没有腾讯视频APP? 立即下载 举报




多边形内角和和外角和 简书




21 7 多边形内角和小學奧數三年級幾何 Youtube
初等幾何学において、凸でない 単純多角形 (英語版) は、凹 (concave130), 非凸 (nonconvex66), 凹角 (reentrant) であるなどと言う。 凹多角形(おうたかっけい、英 concave polygon )は必ず一つ以上の 凹角 (英語版) な—すなわち、角度が180°より大きく360°より小さい—内角を持つ 。内角の和 三角形の内角の和は \(180°\) 四角形の内角の和は \(360°\) これは小学校で学習しましたし、暗記もできていることと思います。 では、 五角形の内角の和は何度でしょうか。 六角形の内角の和は球面上の三角形の内角の和 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明できました。ここで,任意の三角形に対して面積 s > 0 s > 0 s > 0 なので a b c > π abc > \pi a b c > π が成立します! つまり, 球面上の三角形の内角の和は π \pi π より



试题2 1多边形的内角和 测练 19 1多边形内角和 初中沪科版13版 数学中国网 Mathschina Com



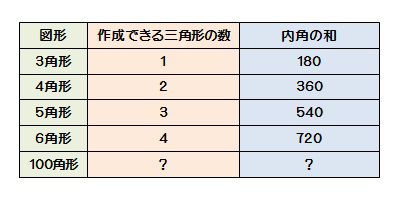
1 完成表格中未填部分 2 根据表中规律 八边形的内角和是度 3 假设图形的边数为a 内角和为s 请你用一个含有字母的关系式表示图形边数与内角和的关系 S 题目和参考答案 青夏教育精英家教网
を作図し、頂角の和を求 めてみよう。どんなこと に気がつきますか。 ,。。。 54。。寒。 ⑥ 本時のまとめと次時の予告 頂角の和が何度であるか、予想(実測)させる 多角形の内角の和の性質についてもふれる n角形Jm飛ばしと一般化してみる2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。点Aから左回りに1つとば しで点を順に結んでいくと星形五角形 ができる。その内角(∠a~∠e)の和 をいろいろな方法で求めてみよう。 H北师大版八年级数学下册多边形的内角和与外角和 第1课时_初二数学_数学_初中教育_教育专区 北师大版八年级数学下册 北师版 八年级 下册 第六章 平行四边形 4 多边形的内角和与外角和 (第1课时) f引入新课 f看一看 引入新课 f生活中的平面图形 讲授新课 长方形 三角形 六边形 四边形 八边形 f讲授新课 工人师傅将一个四边形的桌面用 锯子锯掉一个角,还剩几个角? f




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




六角正多边形内角多边形png图片素材免费下载 图片编号 Png素材网
会员中心 vip福利社 vip免费专区 vip专属特权图:三个顶点时的计算公式,from Wikipedia 对于任意 边形,我们也可以类型的把坐标依次写下来,然后就可以根据公式算出这个多边形的面积了。 不过这里有两点需要注意: (1)对于任意多边形,我们看到的只是各个顶点的坐标,是没有标 的,所以这里我们只需要任意指定一个顶点为 ,然后按照 (1) 多角形の内角の和の公式より、 \(n\) 角形の内角の和は、 \(180^\circ (n − 2)\) よって、内角の和 \(1260^\circ\) を代入すると、 \(180^\circ (n − 2) = 1260^\circ\) \(n − 2 = 7\) \(n = 9\) 答え: \(n = 9\) (2) 多角形の外角の和の公式より、



N 边形内角和 西瓜视频搜索




六角正多边形内角多边形png图片素材免费下载 图片编号 Png素材网
上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 1802、根据多边形的内角和公式求外角和为360 3、n边形内角之和为 (n2)*180,设n边形的内角为∠1、∠2、∠3、、∠n,对应的外角度数为:180∠1、180°∠2、180° 180°∠n,外角之和为: (180∠1) (180°∠2) (180°∠3) (180°∠n) =n*180° (∠1∠2∠3∠n) =n*180° (n2)*180° =360°内角の和の公式を導く $2$ つの考え方を確認しましょう。 ① $\textcolor{green}{1}$ つの頂点から対角線を引く 対角線を引くと、六角形なら $4$ 個$(62 個)$の三角形ができます。




五边形内角和 五边形内角和是多少度




多边形的内角和 题型的十种解法 星火网校
我们发现五边形内角和也是360°,那么也就是说多边形内角和都是360° 到这里我们就可以证明内角和外角和的规律 多边形内角和,外角和的规律我们也是可以证明的,但我只能用文字来证明。 内角和 在n边形内任取一点O,连结O与各个顶点,把n边形分成n个三角形,因为这n个三角形的内角的和等于n·180°,以O为公共顶点的n个角的和是360°,所以n边形的内角和是n·180°2×180多角形の内角の和は下の公式で求められます。 角形の内角の和 = 180 × ( 2) 例えば8角形の内角の和は 180 × (8 2) = 1080 と求めます。 内角の和から 角形の を求める これまで 角形の から内角の和を求めてきましたが、逆に内角の和から 角形の を求める外角と内角の和 外角と内角の和に関する関係は是非覚えましょう。 外角=隣り合わない内角の和 外角隣り合う内角=180度 内角の和と三角形の関係は?1分でわかる和の値、証明、外角との関係 まとめ 今回は外角について説明しました。意味が理解頂け



正多边形内角和多边形内角和公式推导方法 尚书坊




各内角には2つの外角があるが,外角の大きさというときには,図3に示すようにそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° になる n角形の多边形内角和公式是什么意思?我算了看,确实被多边形内、外角和公式减去后是外角和360°这两个公式是从何而来,希望有人能 1年前 1个回答 急求多边形计算内角、外角、度数、对角线的条数、的公式麻




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




八角形正多边形内角六边形不规则线png图片素材免费下载 图片编号 Png素材网




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧



多边形内角和公式 多边形内角和公式 多边形 内角 和 公式 早旭阅读网




在知识迁移 问题类化中探索多角形内角和问题 参考网




10多边形的内角和进阶平行四边形初中数学初二 Youtube



1



多角形の内角と外角 思考力を鍛える数学



数学长征 多边形内角和 内角和 几何 三角形 四边形



多边形内角和定理 用3种方法证明多边形内角和定理 400健康




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学



1




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




多角形の内角の和 は何度なのか を説明します おかわりドリル




正多边形内角和公式及定义 快资讯



N边形的内角和是多少 西瓜视频搜索




在知识迁移 问题类化中探索多角形内角和问题 参考网




正多边形形状二十角形内角多边形png图片素材免费下载 图片编号 Png素材网




多角形の内角の和 算数の公式覚えてますか



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育



正多边形内角和多边形内角和公式推导方法 尚书坊




多边形内角和公式正多边形内角和公式及定义 学习问题 100教育家长学院




多边形的内角和与外角和 Ppt Ppt课件下载 人人ppt



数学长征 多边形内角和 多边形 内角和 内角 外角




多边形的内角和怎么计算 蕾蔻网




一个多边形的内角和等于它的外角和的3倍 则它是几边形 A 八边形b 七边形c 六边形d 九边形 知识点分类总结 学习练习题库 魔分题库




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




探索多边形的内角和 三角形平行四边形和梯形ppt课件 Ppt课件下载 人人ppt




J Ypu1izvngvxm



多边形一个内角怎么求 初三网




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




十一角形 十一角形 Zhz Wiki




多边形的内角




正多边形内角二十角十二角png图片素材免费下载 图片编号 Png素材网




多角形の内角の和 算数の公式覚えてますか



多边形内角和定理 快懂百科
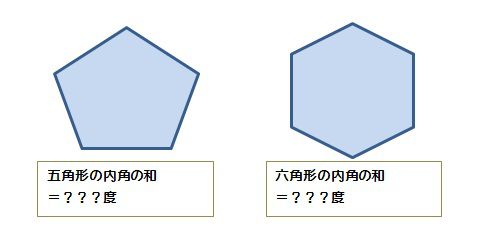



多角形の内角の和 算数の公式覚えてますか



正多边形边数公式 多边形内角和度数公式 尚书坊



正多边形内角和公式 高中数学 七千寻文化 追梦传奇人生



多边形的内角和 三角形ppt 第一ppt



N边形的内角和 西瓜视频搜索



多边形的内角和与外角和 Ppt 第一ppt




多边形内角和怎么求 百度经验



多角形内角 Article




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



如果一个多边形的内角和与外角和相等则此多边形是 X题卡




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




多边形的内角




七年级数学检测 Doc 文档分享网




人教初中数学八上word全册打包教案 第4套人教初中数学八上11 3 多边形及其内角和 教学设计 小库档文库



四下多边形内角和规律 西瓜视频搜索
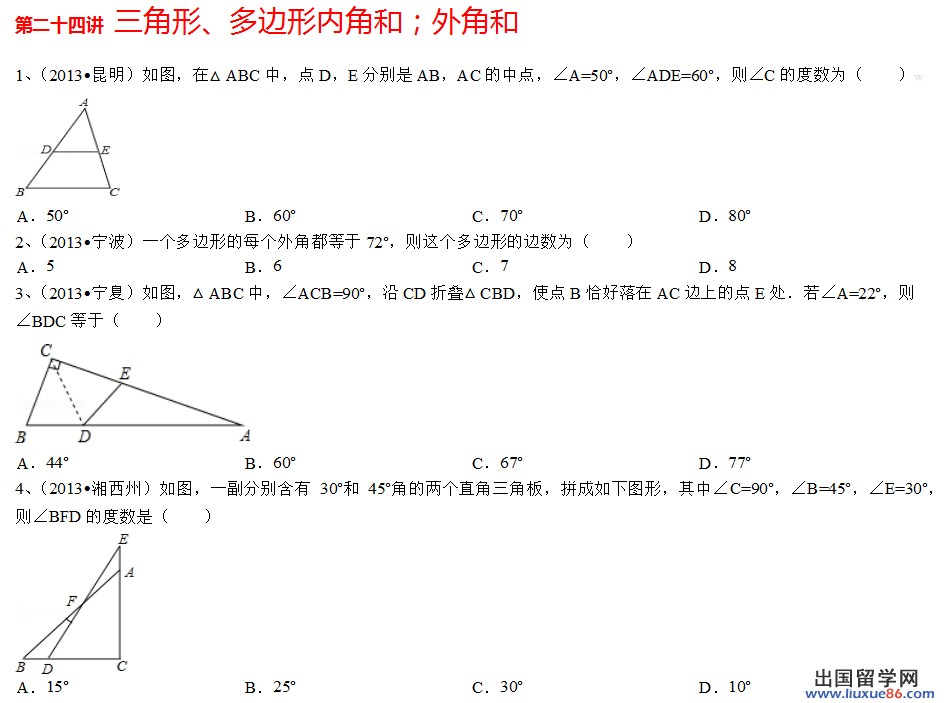



14初三数学三角形多边形内角和外角和



新人教版七下第7 3 多边形及其内角和练习 2 7 3多边形及其内角和 初中人教版 数学中国网




多边形的内角和与外角和 简书




中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



五边形的内角和是多少 多边形内角和怎么求 多边形的内角和公式 秦学教育



1



N 边形内角和 西瓜视频搜索



六边形内角和怎么算 百度经验




多边形内角和公式多边形内角和公式推导 学习问题 100教育家长学院
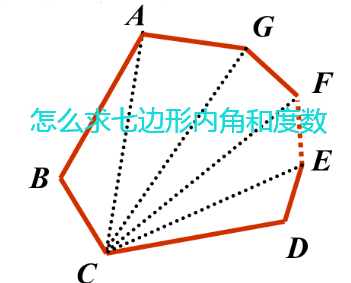



怎么求多边形内角和与外角和的度数怎么求七边形的内角和度数



12边形的内角和是多少 西瓜视频搜索



1




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



多角形内角 Article



五边形的内角和是多少 西瓜视频搜索




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



多边形内角和定理 快懂百科




多角形の内角の和 は何度なのか を説明します おかわりドリル



多边形的内角和与外角和 Ppt 第一ppt



五边形的内角和是360度 西瓜视频搜索



多角形の内角と外角 思考力を鍛える数学



多边形的内角和与外角和 Ppt课件 第一ppt



正多边形内角和 正多边形内角和公式 尚书坊




六边形内角和怎么算 百度经验



多角形の内角の和 算数の公式覚えてますか



多边形的角 禾教 初中数学互动课堂



多角形の内角と外角 思考力を鍛える数学



N 边形内角和 西瓜视频搜索




星形多边形正多边形内角png图片素材免费下载 图片编号 Png素材网



多边形内角和是多少度 初三网




19 1 多边形内角和 初中电子课本网




多边形的内角和与外角和 简书




多边形内角和 搜索结果 哔哩哔哩 Bilibili




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




多边形的内角和与外角和 简书



初中数学多边形内角和 掌握一个公式 学会内外角结合求解边数



多边形内角和的探究 3 6多边形的内角和与外角和 初中湘教版 数学中国网




多边形的内角和与外角和 简书




多边形内角和定理 搜狗百科



0 件のコメント:
コメントを投稿