たすき掛けの因数分解!コツを学んでやり方をマスターしよう! 4乗!?複二次式の因数分解の解き方!途中式をていねいに解説するぞ! 3次式の因数分解!公式とやり方について問題を使って解説! ←今回の記事;「公式を使って因数分解する」よりも先に「共通因数があればくくり出す」という変形をします. 2ab が共通因数だからくれをくくり出します. 6a 2 b−4ab 2 8ab=2ab(3a−2b4) (答) 展開公式・因数分解公式 ① $(ab)^2=a^22abb^2$ ② $(ab)(ab)=a^2b^2$ α (数学Ⅱ,または,教科書非掲載) ③ $(ab)^3=a^33a^2b3ab^2b^3$ ④ $(ab)(a^2abb^2)=a^3b^3$ ⑤ $(abc)^2=a^2b^2c^22ab2bc2ca$ ⑥ $(abc)(a^2b^2c^2abbcca)=a^3b^3c^33abc$ 変形公式 ⑦ $a^2b^2=(ab)^22ab$ ⑧ $a^3b^3=(ab)^33ab(ab)$

因数分解の公式まとめ一覧とその活用例 アタリマエ
数1 因数分解 公式
数1 因数分解 公式- 素数とは、 その数自身と、1以外 に 約数を持たない自然数 (ただし1を除く)のこと。 順番に見ていくと何が素数か分かりやすいかも。 こんな感じ。 素因数分解とは 素因数分解とは、ある正の整数を 素数の積の形 で表すこと。 因数分解の素数バージョン。 4因数分解① 素因数分解 共通因数による因数分解 公式を利用する因数分解① 5因数分解② 公式を利用する因数分解② 公式を利用する因数分解③ 因数分解まとめ 因数分解の応用問題①「1回で終わらない」 因数分解の応用問題②「展開+因数分解」 因数分解の応用問題③「文字の置き換えを




中3 展開と因数分解13 公式を使う因数分解1 予習 中学数学の勉強に
和と差の積の形の因数分解 和と積の数に注意する因数分解 ポイント1 平方の形の因数分解 2 a +2ab +b2=(a +b)2 乗法公式① 上の公式に数字を 因数分解の公式1:x 2y 2 =(xy)(xy) 中学生の皆さんが真っ先に身に着けている公式が x 2 y 2 =(xy)(xy) です。 後に紹介する2種類の公式ほど長いわけでは無いため、この式だけは身につけているというパターンが多いのが特徴です。 1:たすき掛けとは? まずは因数分解におけるたすき掛けとは何かについて解説します。 たすき掛けはイメージが非常に大切ですので、ぜひ本章でたすき掛けのイメージをしておきましょう! 例えば、 ax 2 bxc が (アxイ)(ウxエ) に因数分解できたとしましょう。
乗法公式を使った因数分解 (x+a)(x+b)のタイプの乗法公式を見てみましょう。 x 2 +(a+b)x+ab=(x+a)(x+b)Try IT(トライイット)の因数分解の公式3 (x+a)(x+b)の逆の例題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。 今回は、整式の展開と関係の深い整式の因数分解です。 展開と因数分解の関係は、互いに逆の操作になります。ですからセットで学習するのが効率的です。 関連記事 数と式|整式の展開と乗法公式について数と式|
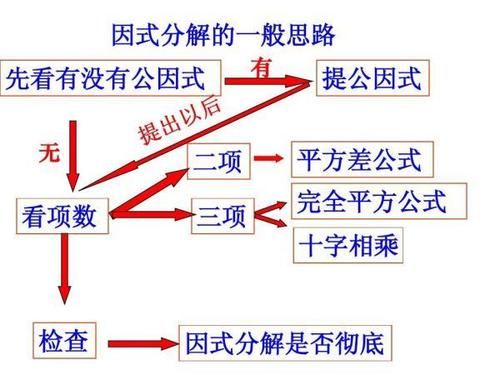
因数分解の4つの基本公式 因数分解についての,基本的な4つの公式を書きます. これらは展開の4つの基本公式で右辺と左辺を入れ替えたものですから,本質は展開のときと全く変わりません. やはり意識するべきことは ( x a) ( x b) の a と b を見て「積多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後 はじめに 因数分解とは、「足し算・引き算で表されている数式をかけ算の形に変形する」ことです。 数学の色んな場面で出てきます。 そんな因数分解には、公式だけでなく早く計算できる解き方があります。 今回の記事では、「因数分解とは何か?」という基礎的な内容から、解き方の解説や練習問題まで載せています。



因式分解 公式法 雪花新闻




中考考点老生常谈问题 因式分解01 及相应的解答题 每日头条
のように、 の2次の項、1次の項、定数項でできている式は、 公式1~3 を使って因数分解をします。 では、 和が、積が になる2つの数を見つけます。 なので、2つの数は と です。 公式1 で、 とすればよいのです。 例1 和が、積が → と 例2 和が、積が → と 例3因数分解(公式1) 1次の式を因数分解しなさい x 2 5x6 x 2 9x x 2 4x3 x 2 6x8 x 2 7x6 x 2 10x16 2次の式を因数分解しなさい x 23x2 x 25x6 x 29x x 25x4 x 27x6 x 210x16 3次の式を因数分解しなさい x 2 x2 x 2 2x3 x 22x8 x 22x35 x 2 3x40 x 28x91)因式分解与解高次方程有密切的关系。 对于一元一次方程和一元二次方程,初中已有相对固定和容易的方法。 在数学上可以证明,对于一元三次方程和一元四次方程,也有固定的公式可以求解。 只是因为公式过于复杂,在非专业领域没有介绍。对于分解因式,三次多项式和四次多项式也有固定




2x 2 X 1因式分解




一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 雪花新闻
因数分解1「公式の確認」 今回のテーマは「因数分解」です。因数分解を5回にわたって解説していきます。 因数分解は、高校数学において基礎中の基礎と言えるところです。だから、当然しっか りと理解しておかないとダメですよ。その前に、まず基本的な因数分解の公式を確認します。 因数分解の公式は、中学3年生で学習するものは、以下の通りです。 a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2 x2+(a+b)x+ab=(x+a)(x+b) a2-b2=(a+b)(a-b) 高校1年、つまり数Ⅰで新しく学習するものは、適当な公式を用いて,次の式を因数分解せよ。 \ 10 次の式を因数分解せよ。 de d e de de d e \ de\ 11 次の式を因数分解せよ。 数学Ⅰ 数と式(因数分解) 演習プリント




衝撃の解答 数検1級の公式解答も間違ってた伝説の因数分解がヤバすぎた Youtube




因式分解经典解析 人人焦点
因数分解の基本公式 サクッと確認してみてください! x 2 ( a b) x a b = ( x a) ( x b) a c x 2 ( a d b c) x b d = ( a x b) ( c x d) x 2 2 x y y 2 = ( x y) 2 x 2 − 2 x y y 2 = ( x − y) 2 x 3 3 x 2 y 3 x y 2 y 3 = ( x y) 3 x 3 − 3 x 2 y 3 x y 2 − y 3 = ( x − y) 3 x 3 y 3 = ( x y) ( x 2 − x y y 2) x 3 − y 3 = ( x − y) ( x 2 x y y因数分解 (公式2) 1 次の式を因数分解しなさい x2 6x9 x2 8x16 x2 10x25 x2 4xy4y2 a2 2abb2 x2 14xy49y2 2 次の式を因数分解しなさい x2 4x4 a2 2a1 m2 6m9 x2 8xy16y2 a2 12ab36b2 x2 14x49 31次式の積の公式の逆利用 3 x2 (b d)x bd = (x b)(x d) 4 acx2 (ad bc)x bd = (ax b)(cx d) まず、簡単な例として x2 5x 6 の因数分解の手順を考えてみよう。 STEP1 x2 6 展開して x2 5x 6 になる1次式の積を考えるため、まず上図のように表を書く。 表の



初中因式分解公式大全 万图壁纸网



初中数学因式分解常用解法有哪些
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 因数分解の公式はよく教科書にわかりやすく載っていますが、複素数をつかった因数分解の公式はあまり載っていません。 最も簡単な例は、\(\displaystyle a^2b^2\)の因数分解です。 3乗動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




因数分解の公式まとめ一覧とその活用例 アタリマエ




3次式の因数分解 公式とやり方について問題を使って解説 Youtube
因数分解是将一个正整数写成几个约数的乘积,在代数学、密码学、计算复杂性理论和量子计算机等领域中有重要意义 1 。因数分解的关键是寻找因子(约数),而完整的因子列表可以根据约数分解推导出,将幂从零不断增加直到等于这个数。例如,因为45= 3×3A n − 1 a^n1 a n − 1 が (a − 1) (a1) (a − 1) の倍数であることが瞬時に分かります。 1 3 n − 8 n 13^n8^n 1 3 n − 8 n が 5 5 5 の倍数であることが瞬時に分かります。 フェルマー数の漸化式が導出できます。→フェルマー数とその性質;具体例で学ぶ数学 > 計算 > 因数分解公式一覧(全22個) 最終更新日 ~中学数学で最初に習う、基本的な公式~ x 2 ( a b) x a b = ( x a) ( x b) x 2 2 x y y 2 = ( x y) 2 x 2 − 2 x y y 2 = ( x − y) 2 x 2 − y 2 = ( x y) ( x − y) ~たすきがけの公式~ a c x 2 ( a d b c) x b d = ( a x b) ( c x d)




因式分解 基础知识 六年级奥数可看 每日头条



2x 2 X 1因式分解
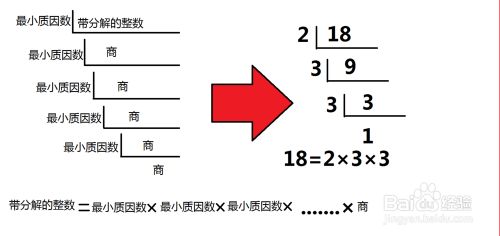
本題の素因数分解へ 因数と素数の説明は理解できましたか? 文字通り、素因数分解は、 素数で分解(因数で分解なので掛け算の形) にする事です。因数分解は、方程式や関数について考える上で重要な概念の一つである。 たとえば次のように左辺を右辺へ変形することをさす。対して、右辺を左辺へ変形することは展開という。 = () = () = ( ) これらの場合、1複素数の範囲での解説もお願いします。 xの4乗1の因数分解です =>作者:連絡ありがとう.複素数の範囲での因数分解は数学Ⅱで扱っています. なお,このページの解説に沿ってwxMaximaをインストールし,画面上で空打ちをして入力欄を作ってから




1 4乘法公式与因式分解




高校数学 因数分解公式と3次式の因数分解 受験の月
1つの文字で整理する因数分解:説明・例題・練習問題 対称式・交代式の因数分解:説明・例題・練習問題 複2次式の因数分解:説明・例題・練習問題 公式を利用した高次方程式の因数分解:説明・例題・練習問題 数学Ⅰの目次へ 数学の目次へ 因数分解とは、1 つの整式を複数の整式の積に変形する操作をいいます。 変形後の積をなすもののそれぞれを因数と呼びます。 ※整式:単項式と多項式を合わせたもの。 例えば次の例を見てみましょう。 これは最も簡単な因数分解の 1 つです。 pa qa という整式が、p q という整式と a という整式の掛け算に変形されています。 先ほどよりは難しい形をしてい <因数分解のやり方をこの1記事でマスター> 数学の計算や、問題を解いていく上で「基本中の基本」となる『因数分解』ですが、数Ⅲや数Ⅱbで点数が取れないことの根本原因が、 因数分解などの基礎事項であった、 ということは非常に多いのです。 ぜひこの記事をじっくり読んで、因数分解
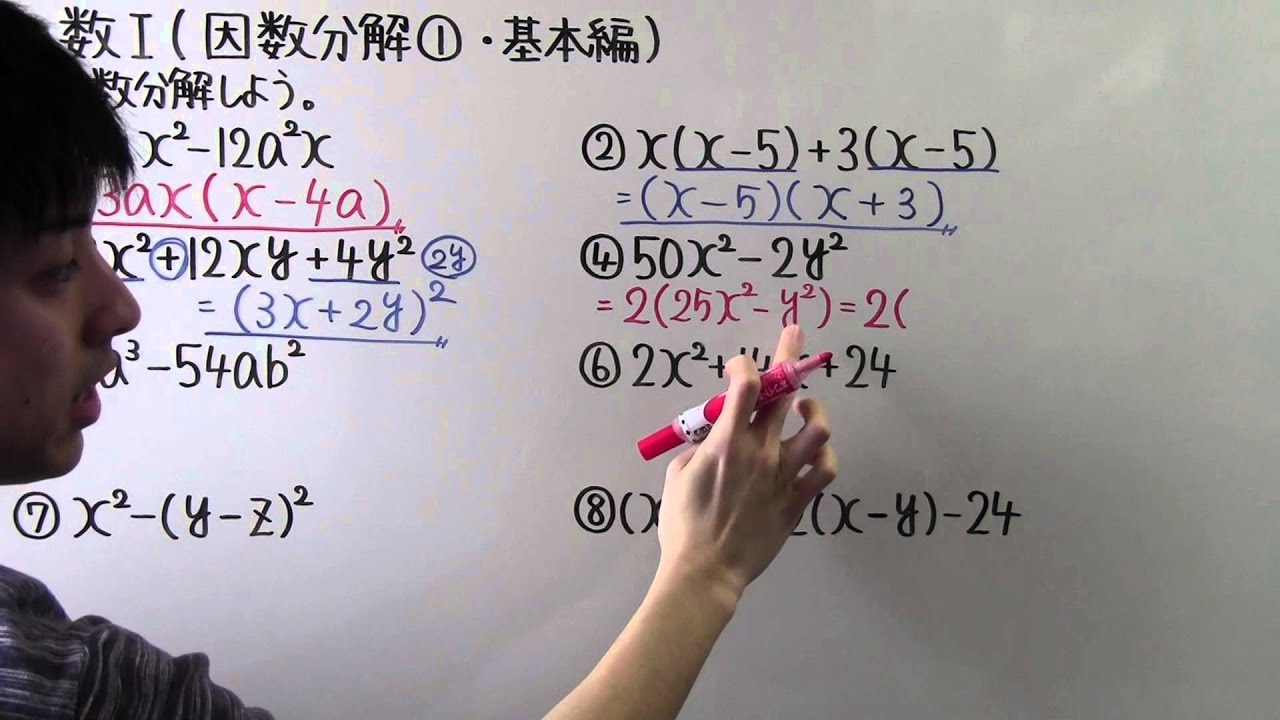



高校数学 数 8 因数分解 基本編 Youtube



7 9 5 因式分解 3 公式法 完全平方公式 哔哩哔哩 つロ干杯 Bilibili
§1 数 と 式 1 因数分解 5ab 2 のように,いくつかの文字や数を掛け合わせてできる式を単項式といい,また,4x 2 6x7のように,いくつかの単項式の和として表される式を,多項式という。 単項式と,多項式をあわせて整式と呼び,次数がnの整式をn次式という。



分解素因数的方法 百度经验




初一数学下册乘法公式 因式分解word版下载 Word模板 爱问共享资料




3乗の因数分解 展開 公式 理系ラボ



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス




公式法分解因式 因式分解运用公式法 环球信息网



初中数学丨因式分解12种方法 做题会这么多绝对够




3次式の因数分解 公式とやり方について問題を使って解説 数スタ




因数分解で必要な公式を集めてみました 高校数学の達人 河見賢司の日記



初中数学 弄懂这几道题 从此使用完全平方公式因式分解得心应手




数字1 既不是质数也不是合数的几何证明 合数三角形 N Pq的分解公式 哔哩哔哩




4因式分解zhang 4下载 Word模板 爱问共享资料




因式分解 易错点辨析 参考网



初二数学 7种方法 让你再也不怕因式分解




初中数学 初一数学 因式分解 练习题 精选 Doc 蚂蚁文库




高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト




因式分解法 數學中用以求解高次一元方程的一種方法 把方程的一側的數 包括 華人百科



初中数学 因式分解方法介绍及真题训练 收藏好 考试提分用得上 相关



初二数学知识点 因式分解的方法之运用公式法 因式分解 中考网




求一个数所有的因子个数和因子和 Tang7o的博客 Csdn博客



乘法公式 整式的乘除与因式分解ppt课件2 第一ppt




完整版 因式分解公式大全下载 在线阅读 爱问共享资料



1




高校数学 数 11 因数分解 3次式の公式編 Youtube
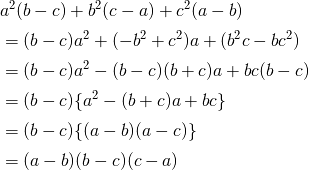



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局



关注因式分解新题型 1 3公式法 初中湘教版 数学中国网



华师大版 初二数学因式分解 知识点及经典例题详解 Doc 教育文库 教育资源网 新时代文库www Xsdwk Com 教育文库 教育资源网 新时代文库www Xsdwk Com



因式分解练习 不要墨守成规 数学的特点就是变通 方法




因式分解公式解因式分解 Oouzd



1



悟空问答 18的因数有几个 14个回答




因式分解常用公式 因式分解的解题技巧 星火网校




数検1級の因数分解できる 3本勝負 Youtube




1 4乘法公式与因式分解




因数分解の公式まとめ一覧とその活用例 アタリマエ




如何因式分解三次多项式 12 步骤




46 A3 Ab 3 3ab Ab A3b Descubre Como Resolverlo En Qanda



因式分解公式法 腾讯视频



因式分解幽默教学 经典语录大全




初中数学 因式分解成难点 掌握方法更要知道什么时候用 楠木轩




たすき 掛け 因数 分解 基本 たすき掛けを使った因数分解 Amp Petmd Com




因式分解要掌握的7种方法和4种解题思路 太简单了 每日头条




夏まとめ 数学1 因数分解 高校生 数学のノート Clear




因数分解の公式まとめ一覧とその活用例 アタリマエ




初中英语 因式分解的九种方法 知乎




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




中考数学 50道经典因式分解详解例题 知乎



06一元二次方程的解法 三 公式法 因式分解法 巩固练习 提高 K12资源




二项式公式 多项式公式和因式分解 知乎



因数分解とは 1分でわかる意味 公式の一覧 問題 たすきがけのやり方



因式分解知识点总结




二项式公式 多项式公式和因式分解 知乎




中3 式の計算 因数分解 公式編 設計図の選び方と使い方 あとはパズル 教えたい 人のための 数学講座




中3 展開と因数分解13 公式を使う因数分解1 予習 中学数学の勉強に



1




分解例题 初中数学 因式分解的常用方法 例题详解 温迪教育的博客 程序员宅基地 程序员宅基地




1x版八年级数学下册第4章因式分解第3节公式法第1课时教案新版北师大版下载 Word模板 爱问共享资料




Amc 备考助推器 Amc 12 数论板块公式 定理 方法汇总06 哔哩哔哩



初中数学 十字交叉相乘法 先分组再套公式 两道因式分解练习 网易视频




质因数分解 思维训练 Noip知识课堂




因式分解 整式的乘除与因式分解ppt课件2 Ppt课件下载 人人ppt




因式分解7种常考方法下载 Word模板 爱问共享资料




浙教版七年级初一数学下册 因式分解用乘法公式分解因式 教材教案word 牛图文



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス



Q Tbn And9gct1netzzhafcs4qhf Nmky5ubvxgihq1hf9ivroi Ck7rwdiupw Usqp Cau




展開 因数分解は1時間で解けるようになる 外資系コンサルタントが主夫になったら




2 29 541 7919 素数 整数 合数 质数 因数 网易订阅




高校の因数分解公式一覧 たすき掛けや手順 やり方




因数分解の公式 中3 鶴城数人 Note




沪科版七年级初一数学下册 整式乘法和因式分解完全平方公式与平方差公式 教材教案word 牛图文




因式分解要掌握的7种方法和4种解题思路 太简单了 每日头条




初中数学 公式法分解因式 你必须注意两大问题 网易订阅
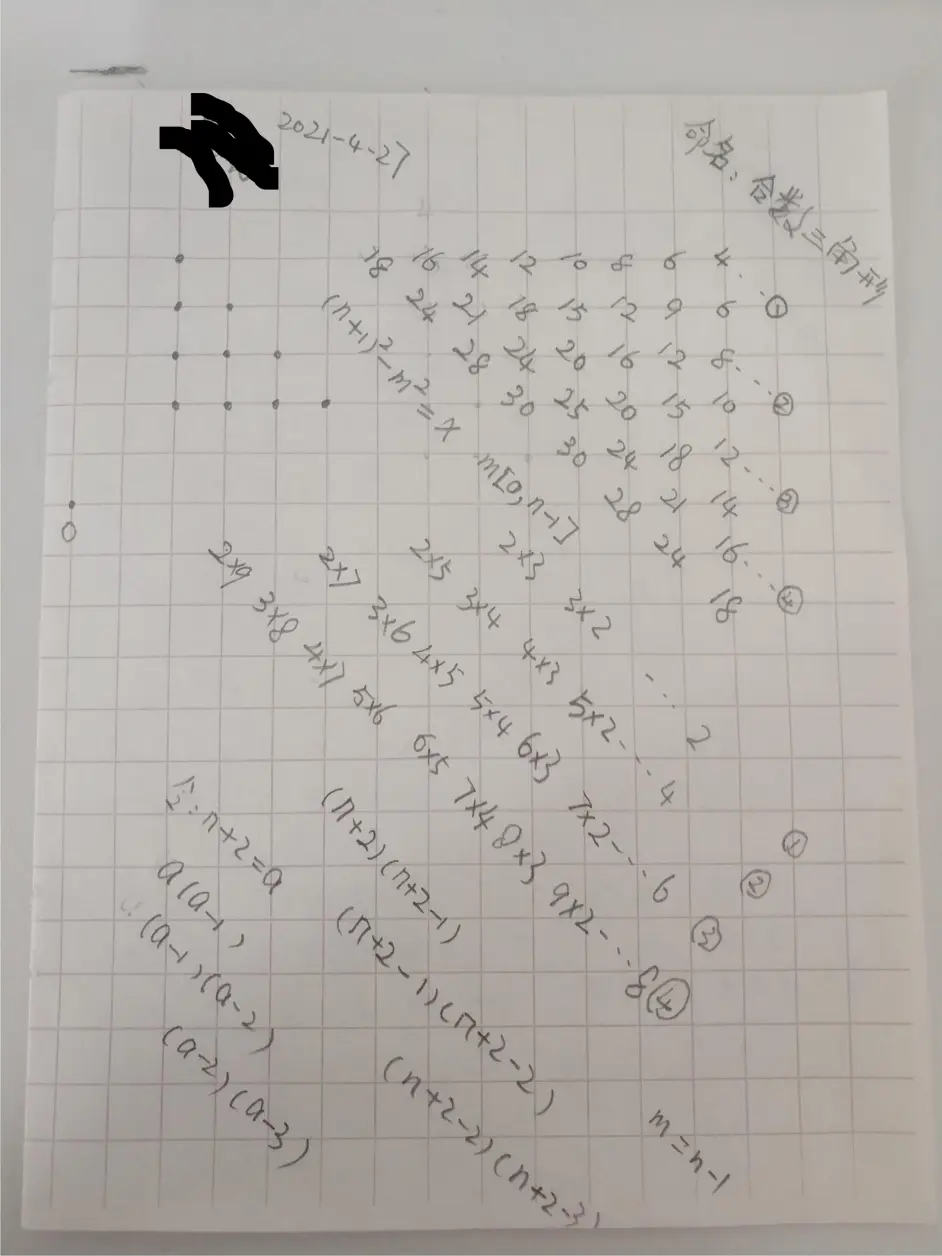



数字1 既不是质数也不是合数的几何证明 合数三角形 N Pq的分解公式 哔哩哔哩



初一数学 因式分解 练习题 沃文网wodocx Com



因式分解的常用方法 11 1因式分解 初中冀教版13版 数学中国网 Mathschina Com




初中数学 初一数学 因式分解 练习题 精选 Doc 蚂蚁文库




乘法公式和因式分解练习题 Doc 牛牛文库niuwk Com



高二数学实系数一元二次方程教案 莲山课件




因式分解公式计算机




一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 雪花新闻
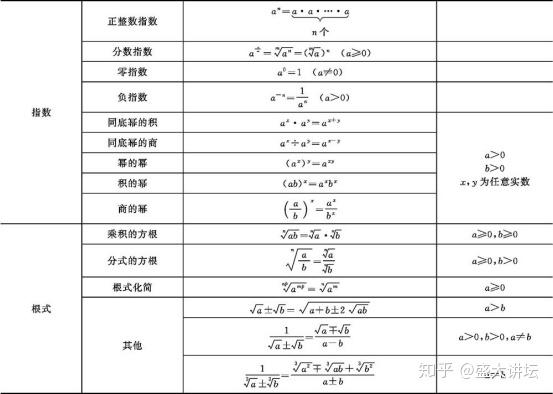



二项式公式 多项式公式和因式分解 知乎




10 5 因式分解 Ppt Download



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス




牛客多校 第四场 B Basic Gcd Problem 质因数分解 程序员大本营




因式分解公式十字相乘



初二数学因式分解 二 运用公式法 例题解析及课后训练 初中数学 学习资料大全 免费学习资源下载



初中常用因式分解公式 学豆中考网 求知网



公式法 因式分解ppt 第1课时 第一ppt




怎么进行因式分解 百度经验



0 件のコメント:
コメントを投稿