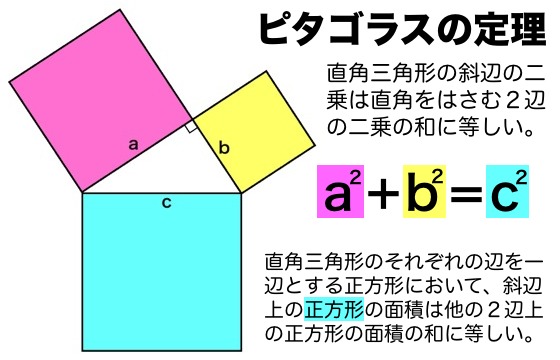
三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ!3 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理(三平方の定理)の証明は、百以上知られている。これに対して、三平方の定理の逆とは?? そもそも、なぜ三三 平方 の 定理 証明 中学生三 平方 の 定理 証明 種類 三平方の定理が、数学が苦手な人でも必ず理解できます。 公式の説明だけでなく、三平方の定理の公式の証明、計算方法と解き方、暗記すべき比と角度、計算問題まで紹介しています。 この記事だけで三平方の定理について美しい 三 平方 の 定理 証明 中学生 三平方の定理について考える1 教科書 大日本図書

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
三 平方 の 定理 証明 中学生
三 平方 の 定理 証明 中学生- 数学三平方の定理が成り立つ三辺の比:最重要7パターン ~受験の秒殺テク(5)~ 絶対におぼえておきたい直角三角形TOP7 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。この図からどのようにして三平方の定理が 導き出されるのだろうか。 ウモクホ数学に匹敵する学問体系を築き上げた 古代中国の学者に思いをはせながら、 証明方沵を考えてみてください。 14....補足2 三平方の定理の三次元拡張




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
三平方の定理の証明 三平方の定理はなぜ成立するのか ありとあらゆる直角三角形に成り立つというのです不思議な気がしませんか 実に様々な証明がありますが 中学生が学習しておくべき最も重要な証明を紹介します 三平方の定理 証明の例 下図のような直角三角形を 4 つを Pythagorean theorem は直角三角形の3辺の長さの関係を表す 斜辺の長さを c 他の2辺の長さを a b と三 平方 の 定理 証明 中学生 三 平方 の 定理 証明 中学生三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイトが得られる。 証明終 122 整数は四つの平方数の和に分解することができる 定理15 全ての正の整数は、四つの平方数の和として表わすことができる n = x2 1 x 2 2 x3 x 2 4 上の定理において02 = 0 も平方数と考えている。よって、0 を除くならば四つ以
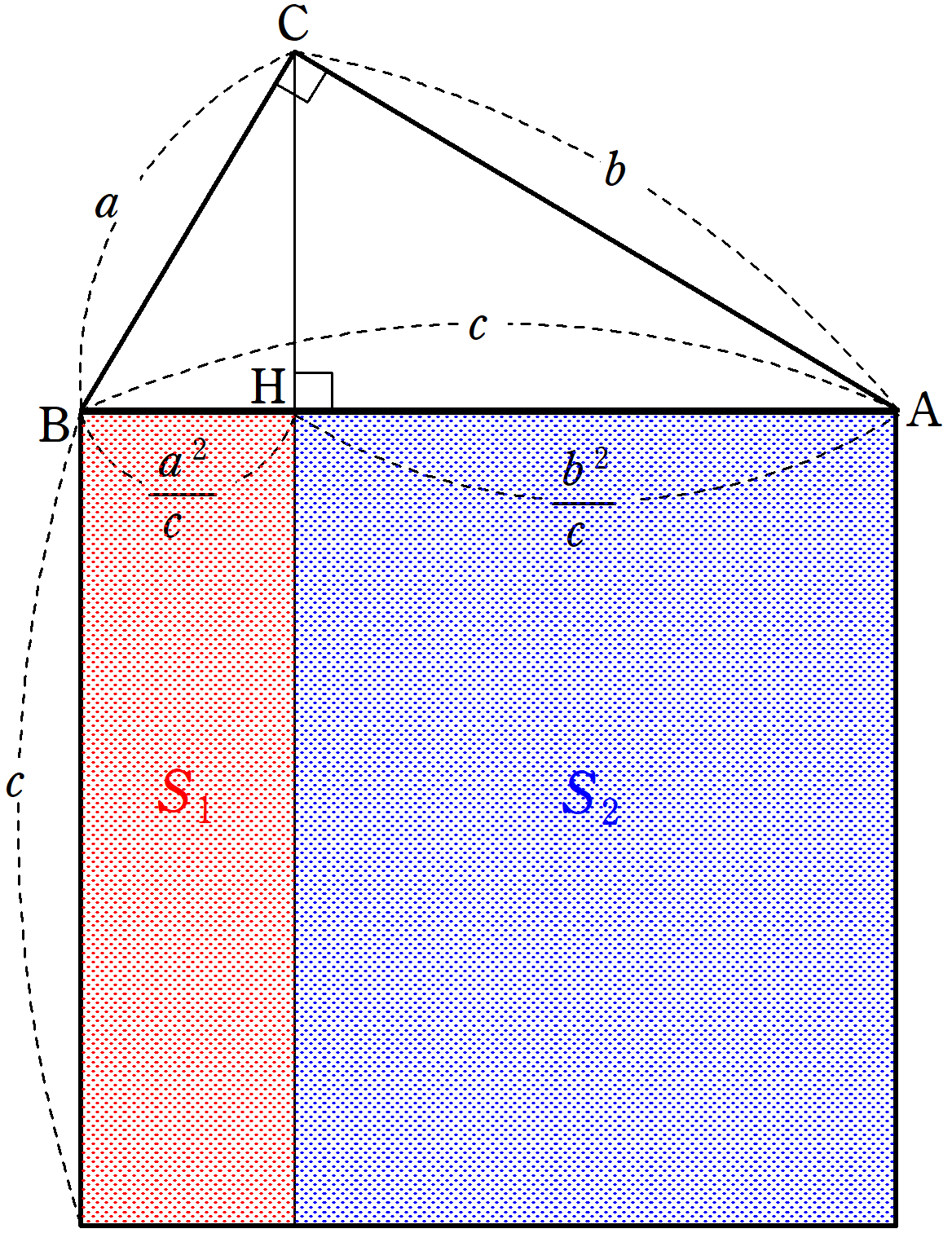
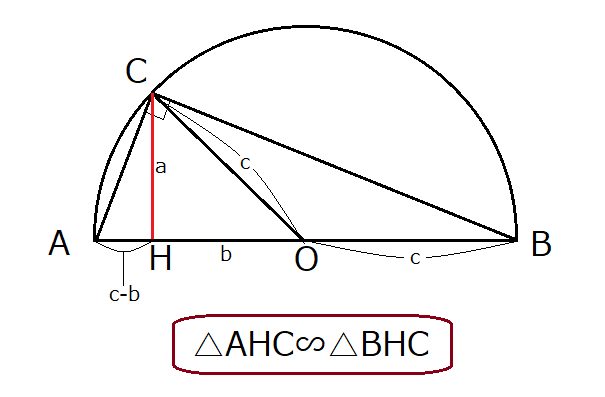
三平方の定理の証明って意外と簡単ですね。 ABCと ACHが相似だから b:AH=c:b 即ち AH=b 2 ABCと CBHも相似だから a:bH=c:a 即ち BH=a 2 だから c=AH+BH=b 2 2 2 +b 2 =c 2 三平方の定理の証明方法は100通り以上あるようです。私自身そんなには知りませんが視覚的証明 初等幾何学 における ピタゴラスの定理 (ピタゴラスのていり、 英 Pythagorean theorem )は、 直角三角形 の3 辺 の長さの関係を表す。 斜辺 の長さを c, 他の2辺の長さを a, b とすると、定理は c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} が成り立つとGaussLegendreの三平方の定理 正整数が三つの平方数の和で書けるための必要十分条件はその正整数が (は非負整数)の形に書けないことである。 三 平方 の 定理 証明 種類高校受験に向けた、中学生の数学で苦手意識をいだきやすいのは証明‼
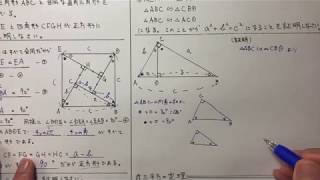
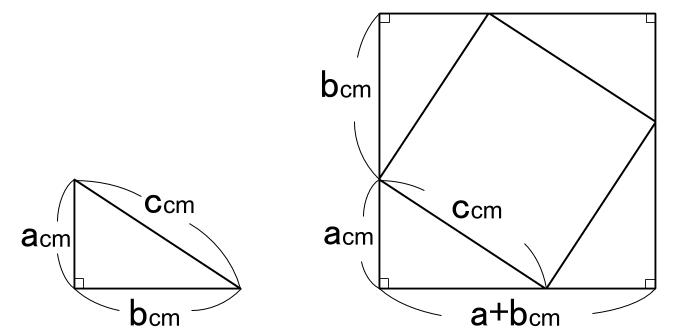
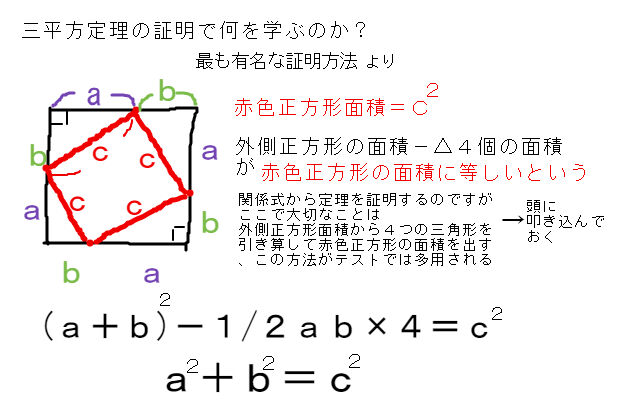
不思議な気がしませんか?実に様々な証明がありますが、中学生が学習しておくべき最も重要な証明を紹介します。三平方の定理 証明の例下図のような直角三角形を \(4\) つをぐるりと並べて、\(1\) 辺の長さが \(ab\) の正方形を作ります。三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べる。 このときa 2 b 2 =c 2 となることを次のように証明した。 空欄ア、イに適切な文字またはが成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく
斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理(三平方の定理)の証明は、百以上知られている。三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは△ABCと合同な三角形4つと正方形EGHCでできている。中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




中学数学 三平方の定理 10 証明 Youtube
三 平方 の 定理 証明 種類 三平方の定理が、数学が苦手な人でも必ず理解できます。公式の説明だけでなく、三平方の定理の公式の証明、計算方法と解き方、暗記すべき比と角度、計算問題まで紹介しています。この記事だけで三平方の定理について 美しい 三 平方 の 定理 証明 中学生 三平方の定理について考える1 教科書 大日本図書 の証明方法 中学数学 三平方の定理 証明 図形的に オンライン無料塾三 平方 の 定理 表 中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生 わかりやすい三角比と基本公式 Irohabook 三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管



中学校数学 証明のコツ 三平方の定理とは




三平方の定理 Instagram Posts Gramho Com
数学 証明の定理まとめ 見れば必ずできるようになる!①中学生の証明part1 9 5 の解き方がわかりません 中3数学 北辰の過去問 19年第3回です 範囲は平方根までです。三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。四平方の定理 角oが全て直角の直角四面体oabcにおいて、面積について s 1 2 s 2 2 s 3 2 = s 4 2 が成り立つ。




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 無料で使える中学学習プリント
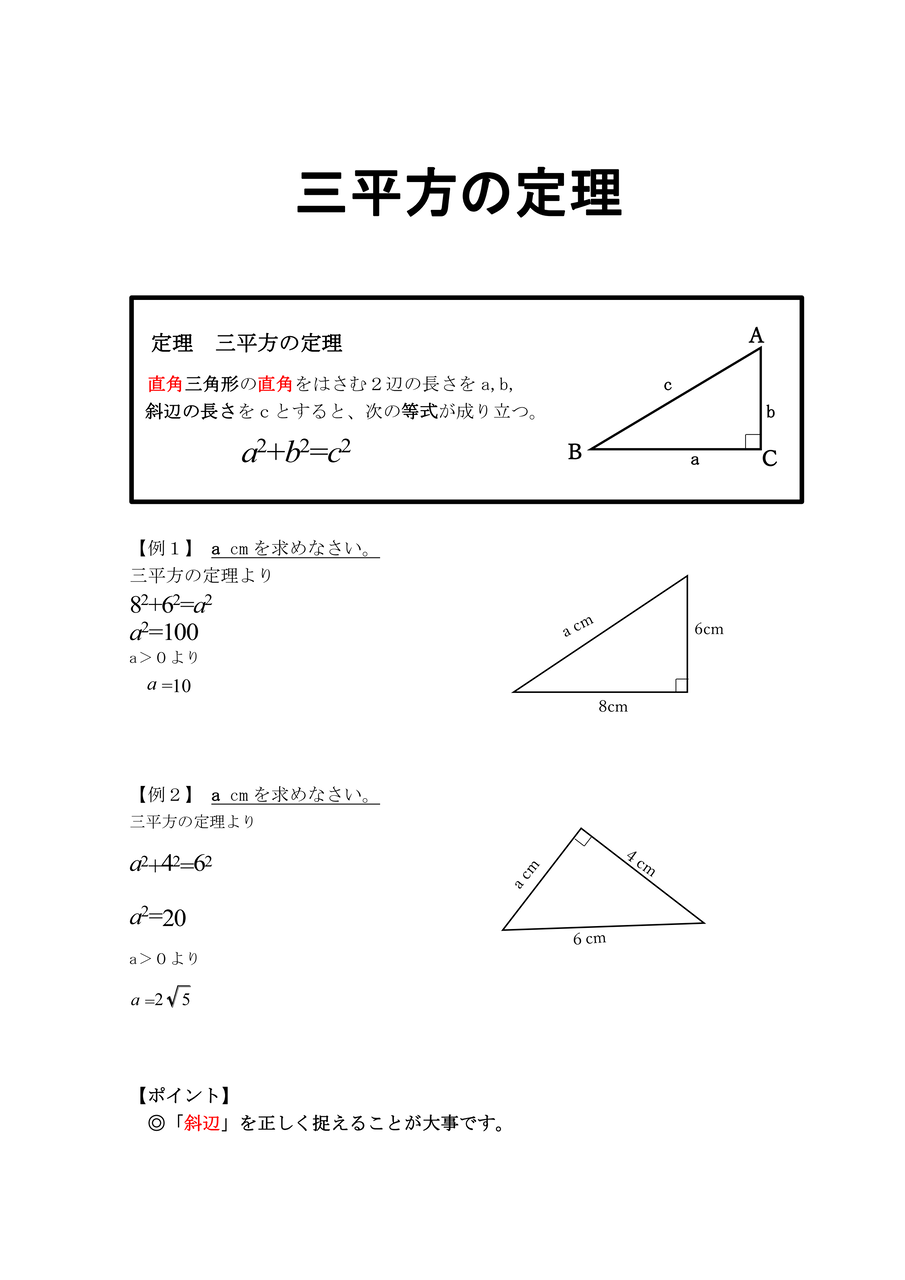
三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。三平方の定理 定理 直角三角形の斜辺を 辺 として、残る直角をはさむ二辺を 辺 および 辺 とした場合に = となる。 (証明) 中学生必見! |数学の無料プリント~中3 三平方の定理~ 中学校数学の中の図形領域で最も最後に学習する「 三平方の定理 」です。 日常生活の中でも使われる数学で有名な定理の一つです。 三平方の定理の歴史、そこから生まれた定理など本当に興味




3 4 5の三角形で 本当に直角ができる Note Board




三平方の定理 高さの求め方編 中3 中学 数学 Youtube
三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の三 平方 の 定理 難問~三 平方 の 定理 証明 中学生 ~ 子供の 必見 公立高校入試対策 最終関門 三平方の定理攻略 後編 みなさんこんにちは現役塾講師のjunですこのシリーズもついに三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理(別名ピタゴラスの定理)とは、底辺が $a$、高さが $b$、斜辺が $c$ である直角三角形において、$$a^2b^2=c^2$$ が成り立つことでしたね。




75 三 平方 の 定理 証明 中学生 最高のぬりえ




うまがお 三平方の定理の証明にチャレンジさせると 意欲的に頑張っていました 中学生の思考は柔らかい すごい 数学的な見方 考え方
四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。注意有些整数不可表示为3个整数的平方和,例如7。




三平方の定理 証明 Pythagorean Theorem Proof With English Subtitles Youtube




三平方の定理の証明 相似を利用した証明2 Fukusukeの数学めも
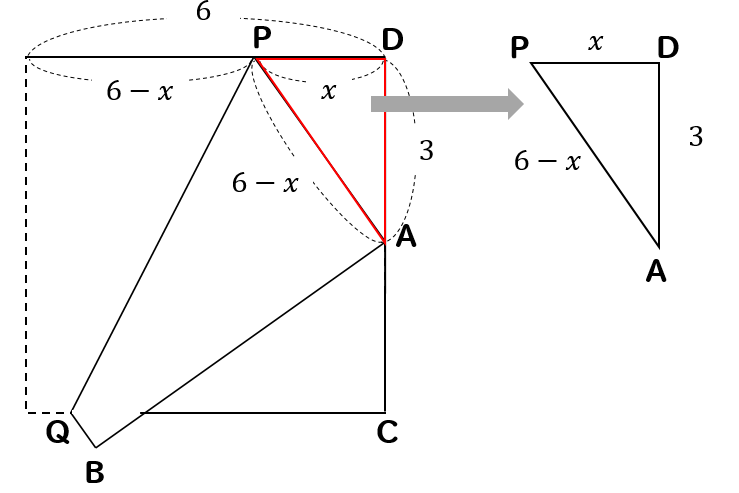



三平方の定理 方程式を利用する発展問題を解説 数スタ




中3 中学数学 三平方の定理 基礎編 中学生 数学のノート Clear



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記




四平方の定理1 空間の中の平面図形の面積と別の平面への正射影 身勝手な主張



1




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張



1




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



中学数学の問題の証明をお願い 円と三平方の定理 下記 Yahoo 知恵袋



面積の問題 小学生 中学生 三平方の定理の証明 みんなの算数クラブ
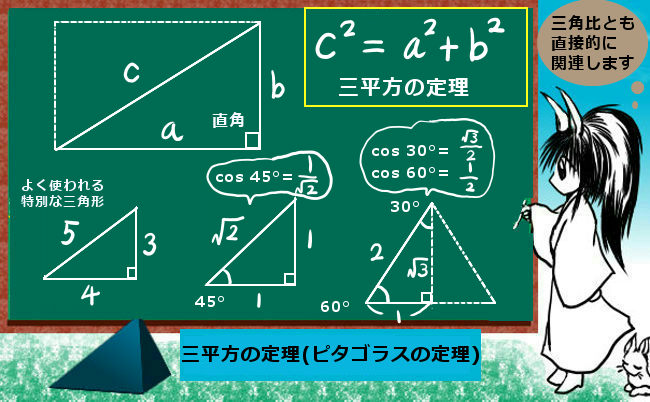



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori
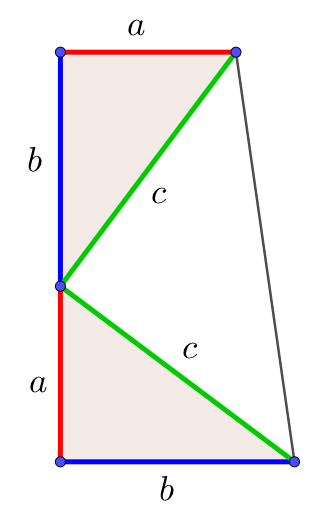



三平方の定理の証明3 大統領の台形 キソカラ
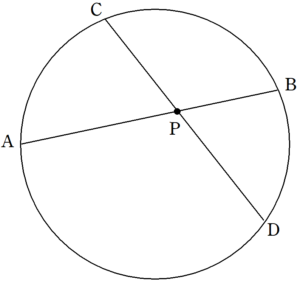



三平方の定理の証明 方べきの定理の利用1 Fukusukeの数学めも
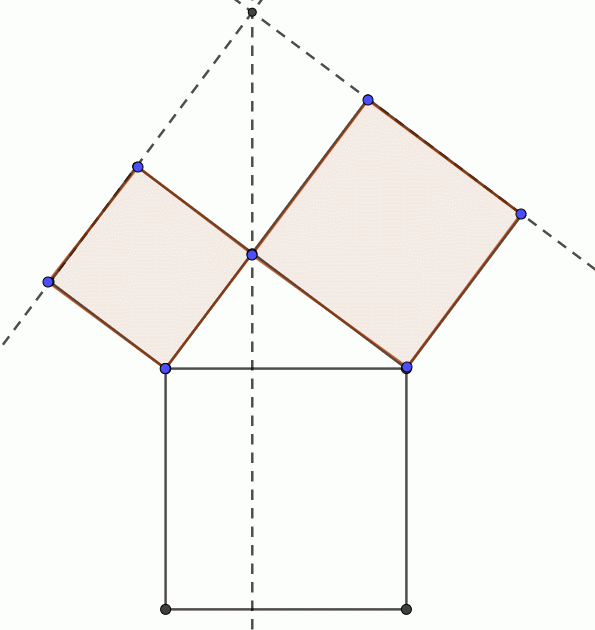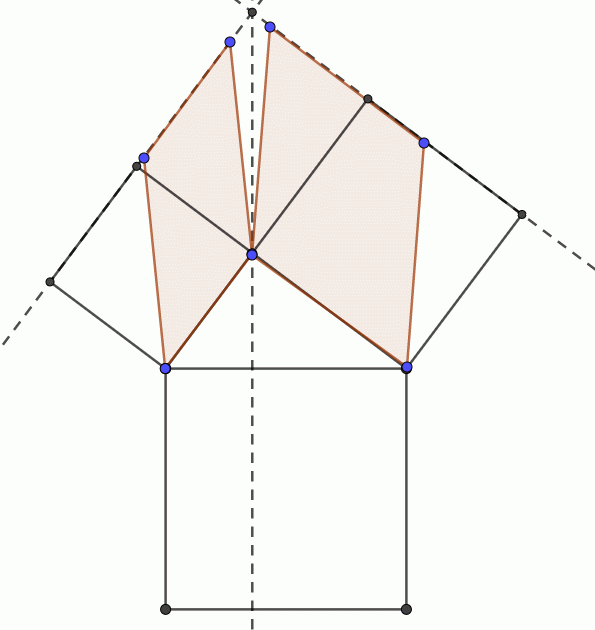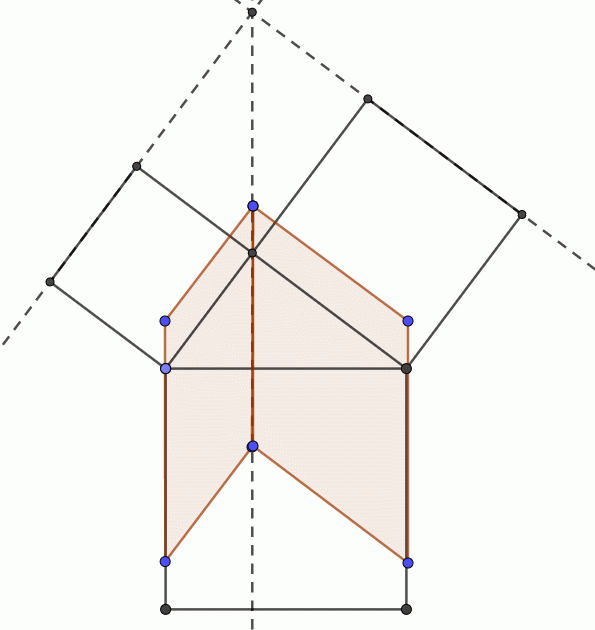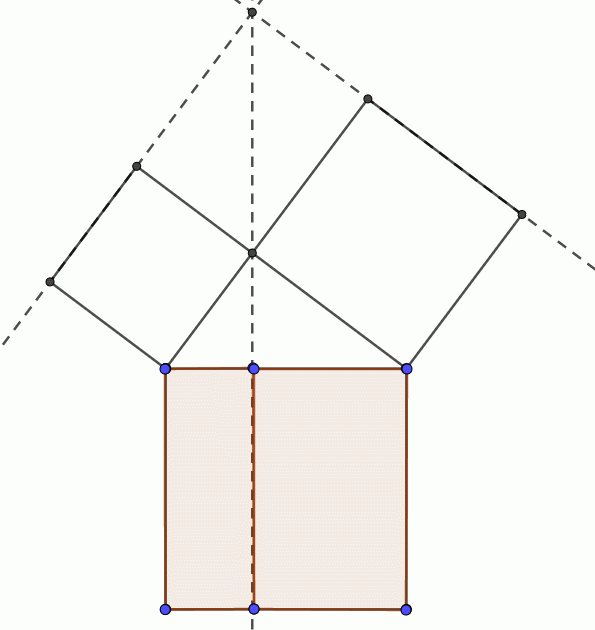



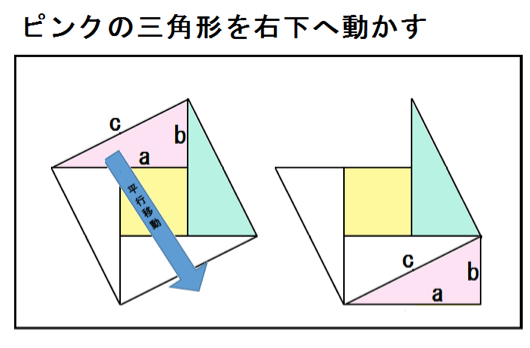
三平方の定理の証明5 だまって平行移動 キソカラ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
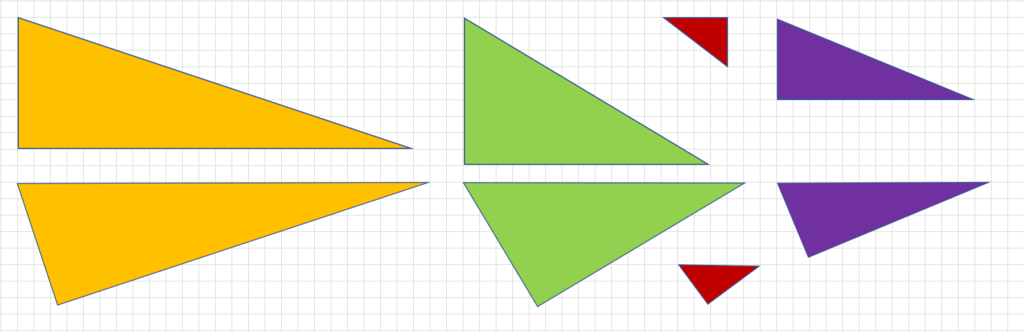



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog
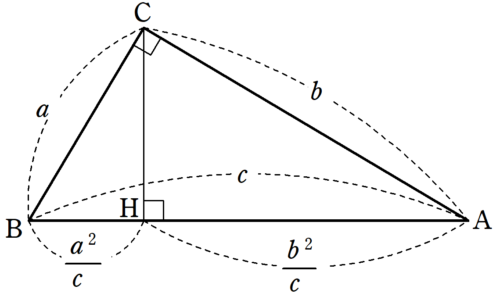



三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



中3数学 三平方の定理1 三平方の定理 証明 すべて無料 星組の中学数学講座




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生
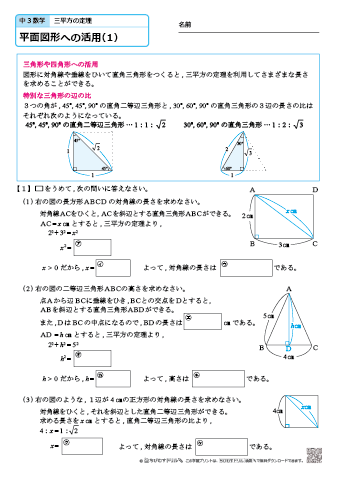



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生




三平方の定理の証明 直感的に分かる図で解説します 数学fun
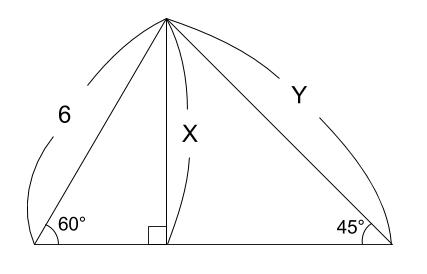



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
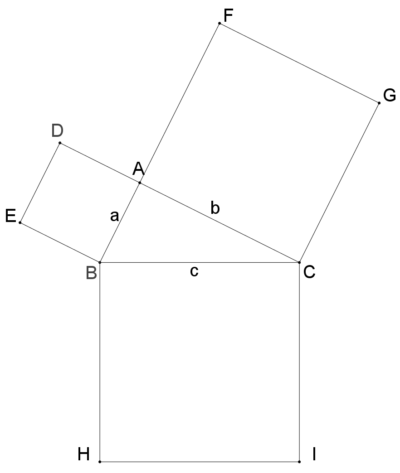



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも



中学数学到達度テスト集中3後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング
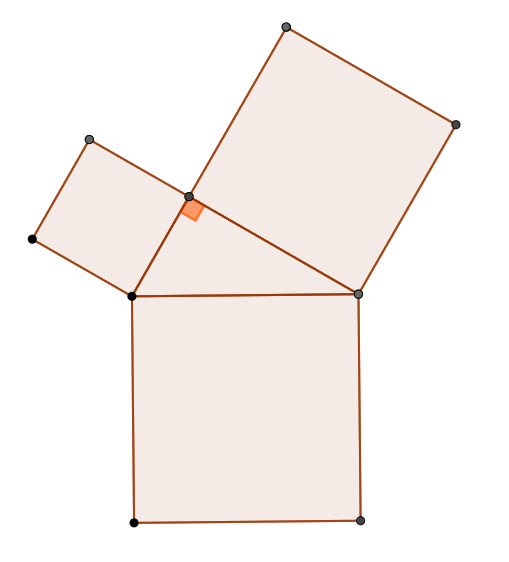



三平方の定理の証明 ピタゴラスの定理とはあまり言いたくない キソカラ
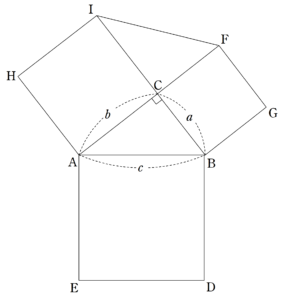



三平方の定理の証明 アン コンディットの証明 Fukusukeの数学めも




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube
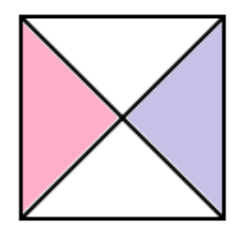



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく




公文数学i教材からj教材へ 公文と小3息子の教育 日常




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月
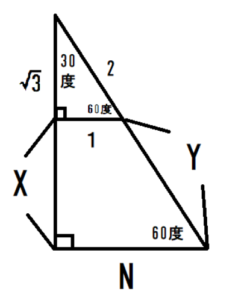



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




50 素晴らしい三 平方 の 定理 証明 簡単 最高のぬりえ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく
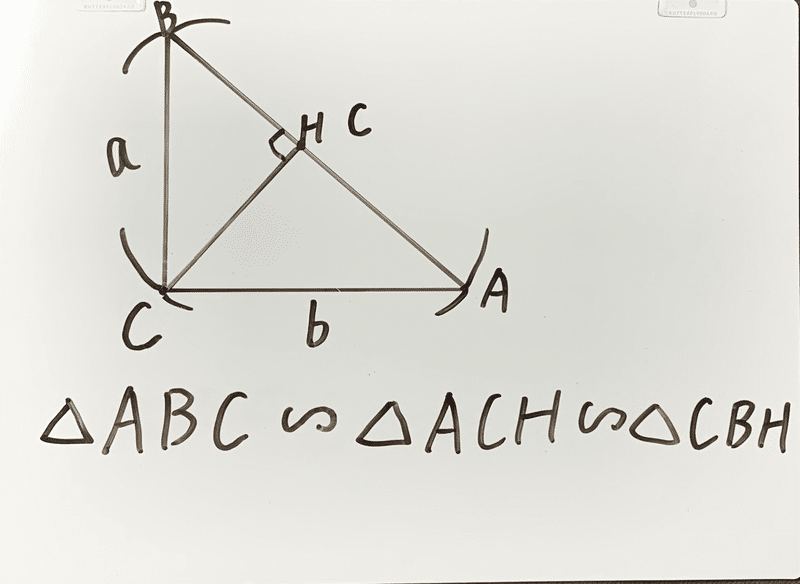



三平方の定理 証明 K Note




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



ピタゴラスの定理とその証明




最新三 平方 の 定理 の 証明 最高のぬりえ



中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
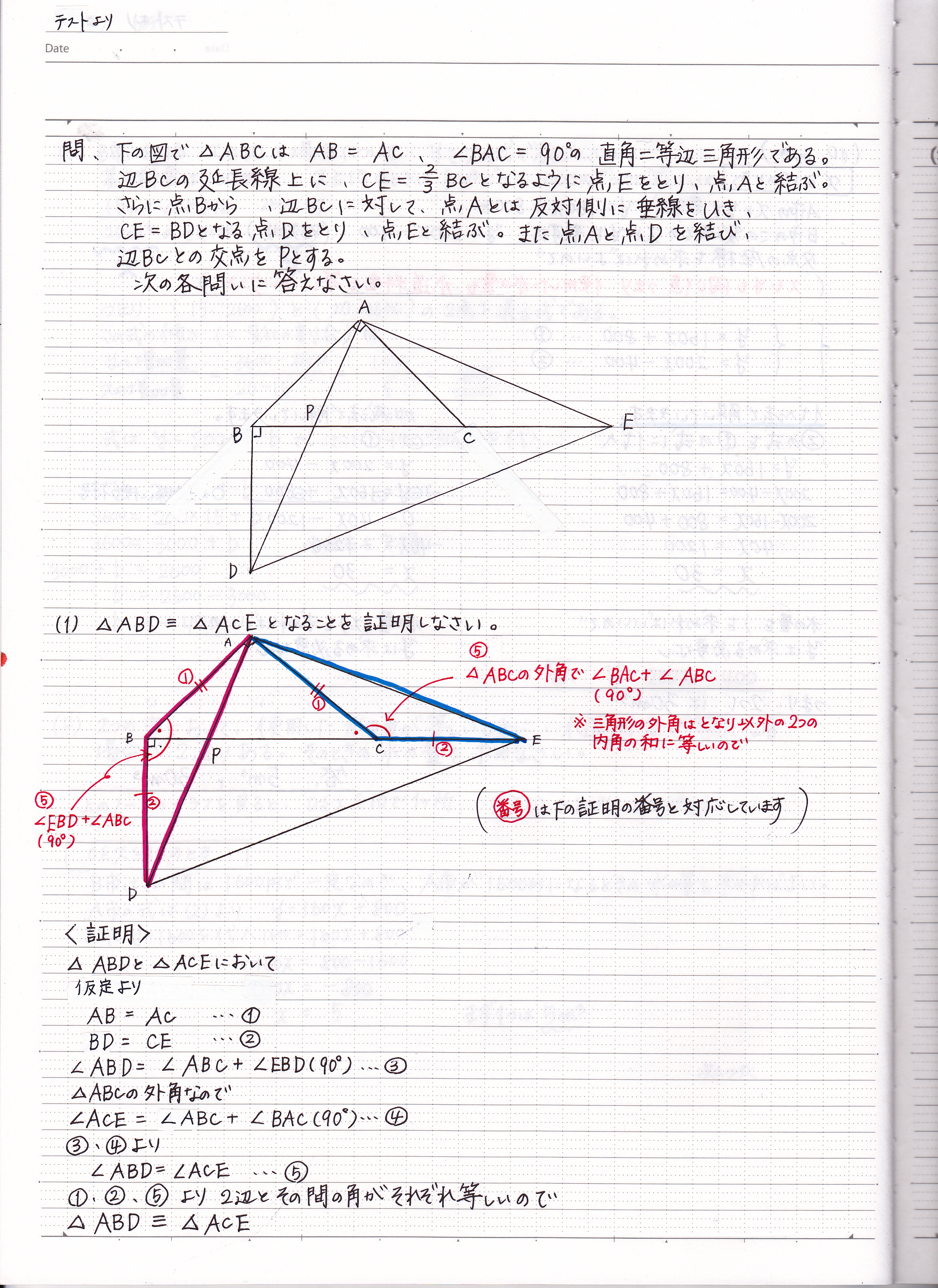



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




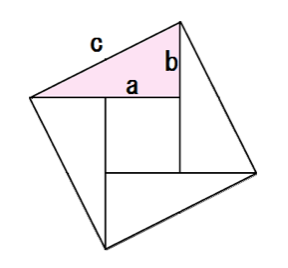
三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト



2




三平方の定理 証明 直角三角形 中3 中学 数学 Youtube




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



中学数学三平方の定理についての質問です この下の問題の解き方が分かりませ Yahoo 知恵袋



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく



1




中学数学 三平方の定理



1



2
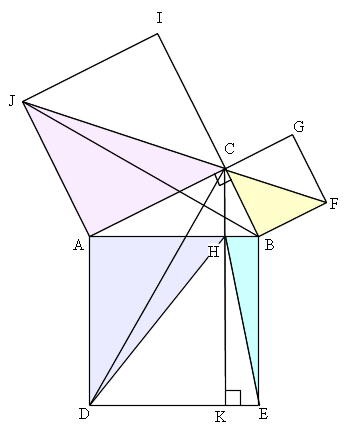



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




三平方の定理 覚えておきたい基本公式を解説 数スタ



三平方の定理




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
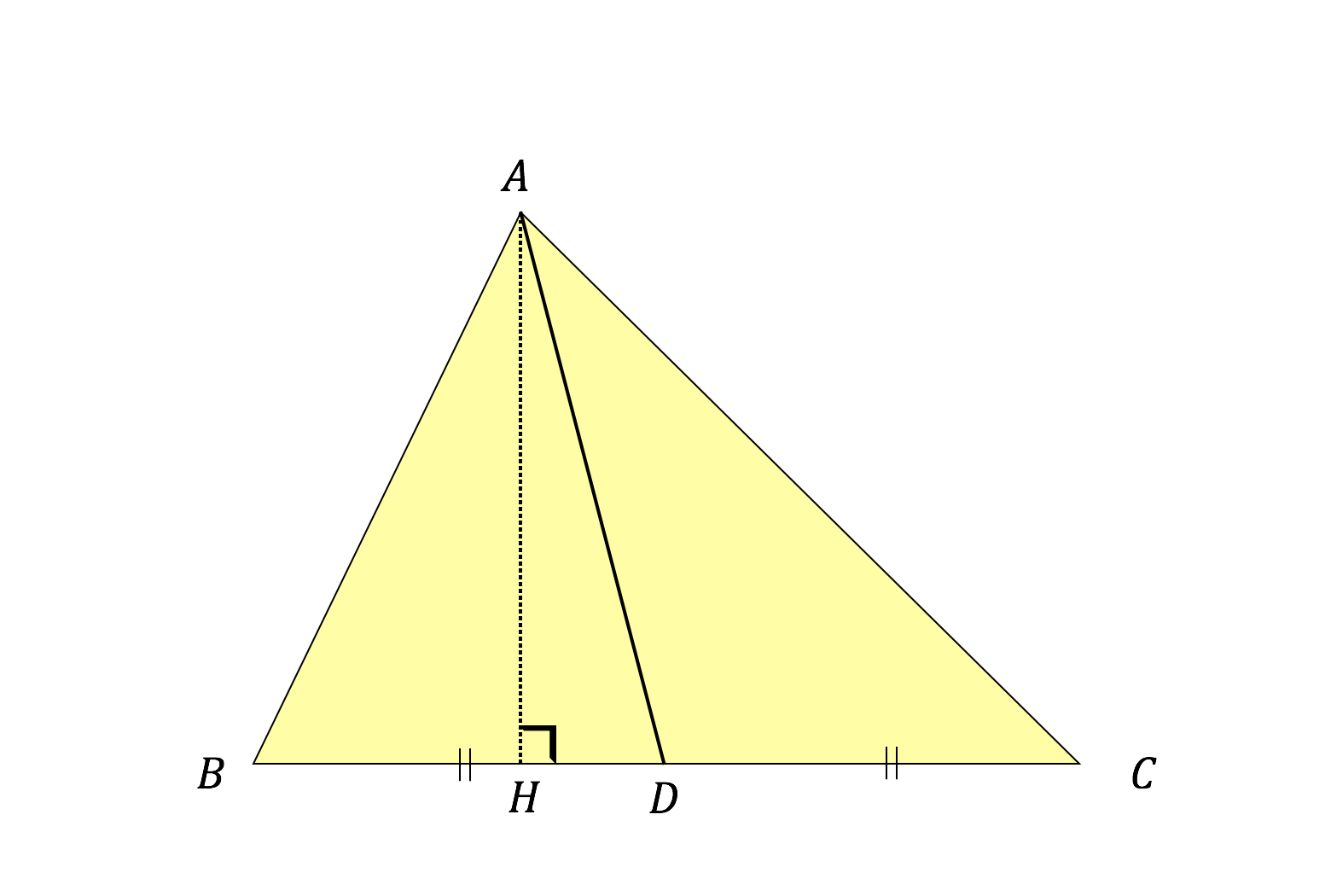



3分で分かる 中線定理 パップスの定理 の証明 問題をわかりやすく 合格サプリ
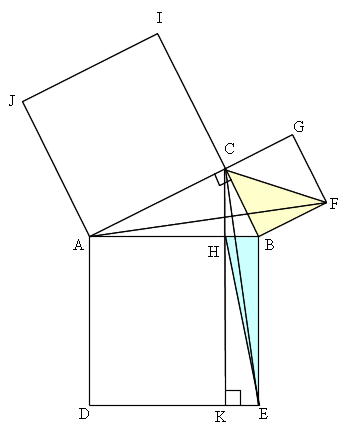



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学
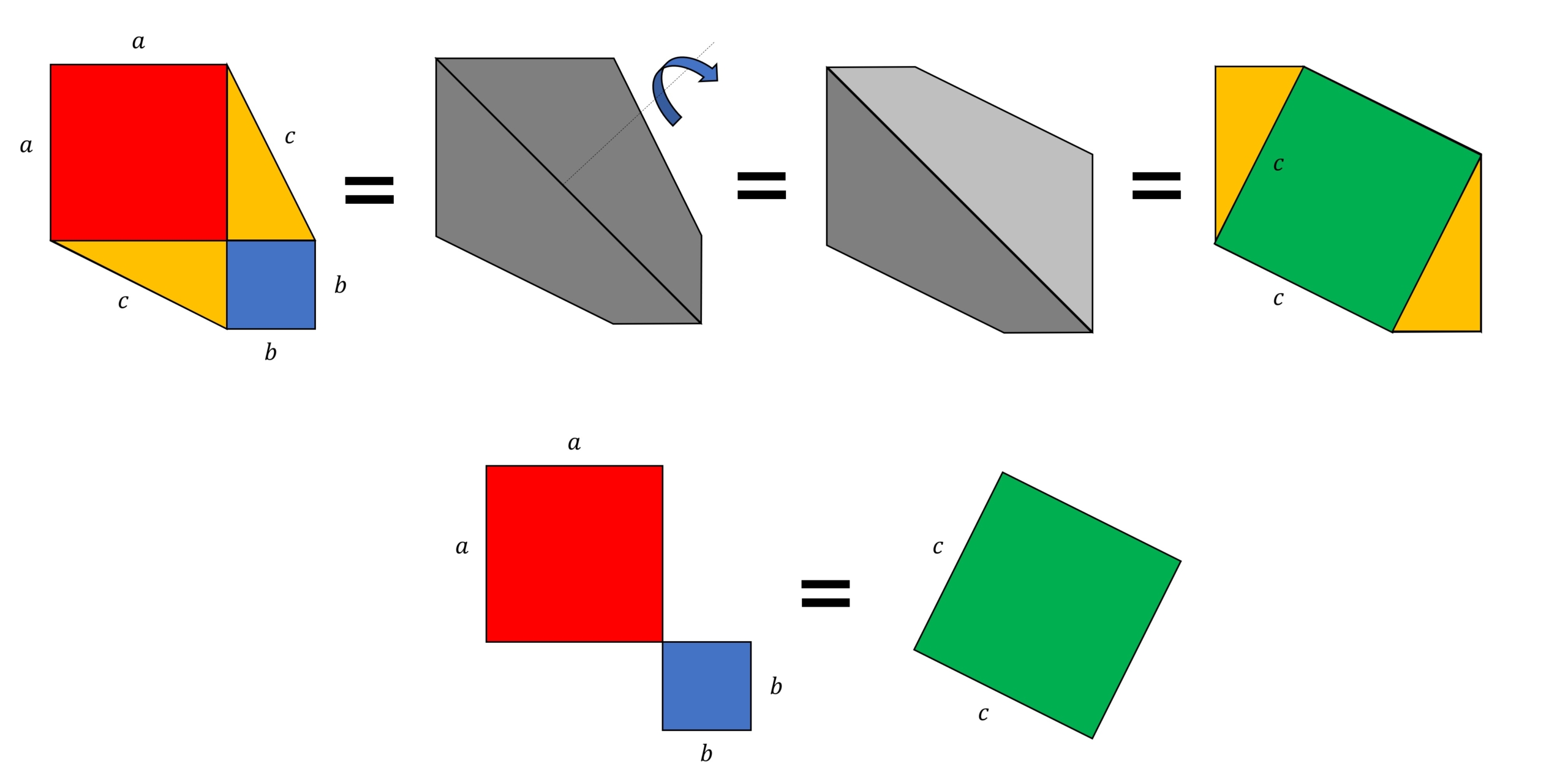



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



ピタゴラスの定理 の思いで チャンネルf




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理です 途中式含め教えてください Clear




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の証明 中学3年数学 Youtube



三平方定理の証明内容で最も覚えておくべきこと 中学数学 理科 寺子屋塾の復習サイト



三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理の最も変わった証明方法はなんですか Quora




中学3年 三平方の定理 のブログ記事一覧 数学のすすめ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




無料 中3数学 発展 応用問題 解答プリント 334 三平方の定理2




ピタゴラスの定理を使って 良い比率の三角形を無限に生み出す おとなぱすた




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2




中3数学 証明で使える定理まとめ 中学生 数学のノート Clear




ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
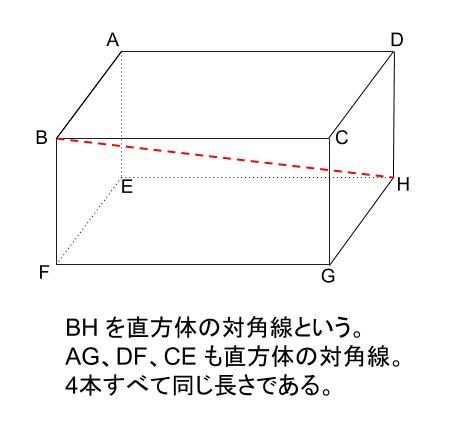



中学数学 直方体の対角線 中学数学の無料オンライン学習サイトchu Su




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



Studydoctor三平方の定理の証明 中学3年数学 Studydoctor




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



中3数学12 三平方の定理2 比の利用 標準問題プリント 問題 334



0 件のコメント:
コメントを投稿